MEV Resistance on a DAG

3y ago•

bullish:

1

bearish:

0

Share

Authors: Dahlia Malkhi and Pawel Szalachowski

Synopsis

Recent work on “Maximal Extractable Value (MEV) Protection on a DAG” explores approaches for integrating “Blind Order-Fairness” – a measure introduced to prevent maximal extractable value (MEV) exploits – into DAG-based approach to BFT consensus.

To meet the high transaction commit-throughput of DAG-based BFT consensus, the performance of Blind Order-Fairness needs to scale as well. If transaction opening falls behind consensus ordering throughput, a backlog of unsettled transactions may grow and grow; and could block clients from being able to submit transactions against the last committed state. This post explains a high-level solution framework and compares different options for implementing blinding/opening in it.

Background

MEV

Over the last few years, we have seen exploding interest in cryptocurrency platforms and applications built upon them, like decentralized finance protocols offering censorship-resistant and open access to financial instruments; or non-fungible tokens. Many of these systems are vulnerable to MEV attacks, where a malicious consensus leader can inject transactions or change the order of user transactions to maximize its profit. Thus it is not surprising that at the same time we have witnessed rising phenomena of MEV professionalization, where an entire ecosystem of MEV exploitation, consisting of MEV opportunity “searchers” and collaborating miners, has arisen.

Daian et al. introduced a measure in [Flash Boys 2.0, S&P 2020] of the “profit that can be made through including, excluding, or reordering transactions within blocks” called the measure miner extractable value (MEV). [MEV-explore] estimates the amount of MEV extracted on Ethereum since the 1st of Jan 2020 to be close to $700M. However, it is safe to assume that the total MEV extracted is much higher, since MEV-explore limits its estimates to only one blockchain, a few protocols, and a limited number of detectable MEV techniques. Although it is difficult to argue that all MEV is “bad” (e.g., market arbitrage can remove market inefficiencies), it usually introduces some negative externalities like:

Network congestion: especially on low-cost chains, MEV actors often try to increase their chances of exploiting a MEV opportunity by sending a lot of redundant transactions, spamming the underlying peer-to-peer network,
Chain congestion: many such transactions finally make it to the chain, making the chain more congested,
Higher blockchain costs: while competing for profitable MEV opportunities, MEV actors bid higher gas prices to prioritize their transactions, which results in overall higher blockchain costs for regular users,
Consensus stability: some on-chain transactions can create such a lucrative MEV opportunity that it may be tempting for miner(s) to create an alternative chain fork with such a transaction extracted by them, which introduces consensus instability risks.

Fair Ordering

In this blog post, we focus on consensus-level MEV mitigation techniques in the classical (or proof-of-stake) BFT setting with a known set of N=3F+1 parties referred to as validators. There are fundamentally two types of MEV-resistant Order-Fairness properties:

Blind Order-Fairness. A principal line of defense against MEV stems from committing to transaction ordering without seeing transaction contents. This notion of MEV resistance, referred to here as Blind Order-Fairness, is used by Heimbach and Wattenhofer in [SoK on Preventing Transaction Reordering, 2022] and is defined as

“when it is not possible for any party to include or exclude transactions after seeing their contents. Further, it should not be possible for any party to insert their own transaction before any transaction whose contents it already observed.”

Time-Based Order-Fairness. Another strong measure for MEV protection is brought by sending transactions to all validators simultaneously and using the relative arrival order at a majority of the validators to determine the final ordering. In particular, this notion of order fairness ensures that

“if sufficiently many parties receive a transaction tx before another tx’, then in the final commit order tx’ is not sequenced before tx.”

This prevents powerful adversaries that can analyze network traffic and transaction contents from reordering, censoring, and front-/back-running transactions received by validators. Moreover, Time-Based Order-Fairness has stronger protection against a potential collusion between users and consensus proposers, because validators explicitly input relative ordering into the protocol. Time-Based Order-Fairness is used in various flavors in several recent works, including [Aequitas, CRYPTO 2020], [Pompē, OSDI 2020], [Themis, 2021], [Wendy Grows Up, FC 2021] and [Quick Order Fairness, FC 2022].

Another notion of fairness found in the literature, that does not provide Order-Fairness, revolves around participation fairness:

Participation Fairness. A different notion of fairness aims to ensure censorship-resistance or stronger notions of participation equity. Participation equity guarantees that a chain of blocks includes a certain portion of honest contribution (aka “Chain Quality”). Several BFT protocols address Participation Fairness, including [Prime, IEEE TDSC 2010], [Fairledger, 2019], [HoneyBadger, CCS 2016], and many others. In layered DAG-based BFT protocols like [Aleph, AFT 2019], [DAG-Rider, PODC 2021], [Tusk, 2021], [Bullshark, 2022], Participation Fairness comes essentially for free because every DAG layer must include messages from 2F+1 participants. It is worth noting that participation equity does not prevent a corrupt party from injecting transactions after it has already observed other transactions, nor a corrupt leader from reordering transactions after reading them, violating both Blind and Time-Based Order-Fairness.

A Framework for Blind Order-Fairness in BFT Consensus

The first line of defense against MEV is to keep transaction information hidden until after a commit ordering is delivered “blindly”. This prevents any party from observing the contents of transactions until the ordering has been committed, hence satisfying Blind Order-Fairness. We now introduce a framework for integrating Blind Order-Fairness protection in BFT consensus, in a classical (or proof-of-stake) setting with a known set of N=3F+1 validators.

The core solution is a standard k-of-n secret sharing approach. For each transaction tx, a user (“Alice”) picks a secret symmetric key tx-key, and sends tx encrypted with it to validators. Secret sharing allows Alice to share tx-key with validators such that F+1 shares are required to reconstruct tx-key, and no set of F bad parties can open it before it is committed (blindly) to the total order. Honest validators wait to commit to a blind order of transactions first, and only later open them. At the same time, before committing a transaction to the total ordering, validators ensure that they can open it.

Disperse/Retrieve. More formally, a sharing protocol has two abstract functionalities, “Disperse” and “Retrieve”. Disperse allows a dealer to disseminate shares of the secret tx-key to validators, with the following guarantees:

Hiding: A set of F bad validators cannot reconstruct tx-key.
Binding: After Disperse(tx-key) completes successfully at an honest validator, any set of honest F+1 validators doing Retrieve(tx-key) can reconstruct tx-key generating a unique outcome.
Validity: If the dealer is honest, then the outcome from Retrieve(tx-key) by any F+1 honest validators is tx-key.

It is worth noting that Disperse/Retrieve does not require certain properties which some use-cases in the literature may need, but not the framework here:

When Disperse completes, it does not guarantee the Retrieve can reconstruct an output value that a dealer commits to.
It doesn’t require that individual shares can be recovered.
It doesn’t require being able to use tx-key to derive other values while keeping tx-key itself secret.

Relaxing these requirements will play an important role below in Approaches 3 and 4.

Approaches for Disperse/Retrieve

Approach 1: Threshold Cryptography

It is straight-forward to implement Disperse/Retrieve using threshold encryption, such that a public encryption “E()” is known to users and the private decryption “D()” is shared (at setup time) among validators. Recall that for each tx, a user chooses a transaction-specific symmetric key tx-key and sends tx encrypted with it. To Disperse(tx-key), the user attaches E(tx-key), the transaction key encrypted with the global threshold key. Once a tx is committed to the total-ordering, Retrieve(tx-key) is implemented by each validator generating its decryption share for D(tx-key). Validators can try applying F+1 valid decryption shares to decrypt tx.

Binding stems from two properties. First, a threshold of honest parties can always succeed in generating F+1 valid decryption shares of E(tx-key). Second, some threshold cryptography schemes allow verifying that a validator is contributing a correct decryption share, hence by retrieving F+1 valid threshold shares, a unique outcome is guaranteed.

Properties:

Requires trusted setup or a (computationally costly) distributed setup of threshold encryption.
About 300μs for Disperse using [TDH2, EuroCrypt 1998] on standard hardware. No extra messages.
About 3500μs for Retrieve in a 6-out-of-16 scheme.

Approach 2: Verifiable Secret-Sharing (VSS)

Another way for users to Disperse(tx-key) is [Shamir’s secret sharing scheme, CACM 1979]. The “vanilla” secret sharing scheme has two ingredients: a sharing function “SS-share(secret s)” creates N values, “SS-combine(F+1 shares)” reconstructs the secret s.

To Disperse(tx-key), a user employs SS-share(tx-key) to send individual shares of tx-key to each validator. A set of F+1 share holders reveal their shares during Retrieve and combine shares via “SS-combine()” to reconstruct tx-key.

Combining shares is three orders of magnitude faster than threshold crypto and takes a few microseconds in today’s computing environment (see Properties notes). However, after Disperse completes with N-F validators, “vanilla” SS-share()/SS-combine() does not guarantee Binding: first, not every set of F+1 honest validators may hold shares from the Disperse phase. Second, retrieving shares from different sets of F+1 validators may result in different outputs from SS-combine().

VSS schemes support Binding through share VSS-verification(share, commit value). VSS-verification() allows validators to check that shares are consistent with a committed value s’, such that any set of F+1 shares applied to SS-combine() results in output s’. When a validator receives a share, it should verify the share before acknowledging it. Disperse completes when there are N-F acknowledgements of verifiable shares, certifying that valid shares are held by F+1 honest validators and guaranteeing a unique reconstruction by any subset of F+1.

It is possible to add a share recovery functionality VSS-recovery(F+1 share-holders) to allow a validator to obtain its individual share prior to Retrieve.

Properties:

No trusted setup is required.
O(N²) communication complexity for Disperse (e.g., using [hbACSS, NDSS 2022], [eAVSS-SC, CT-RSA 2013]). A user needs to send shares privately to individual validators.
O(N²) communication complexity for Retrieve. Optional O(N²) for recovery of missing shares by F+1 honest validators.

Approach 3: AVID-M

VSS provides stronger guarantees than necessary to satisfy the Binding requirement of Disperse/Retrieve. Specifically, Disperse only needs to guarantee a unique secret reconstruction outcome, not success. Borrowing a key technique from [DispersedLedger, NSDI 2022] called AVID-M, validators can completely avoid verifying shares during Disperse (costly). Instead, they verify during Retrieve that the (entire) sharing would have a unique outcome (cheap). This works as follows.

To Disperse(tx-key), a user employs SS-share(tx-key) to send individual shares to validators. Additionally, the user combines all shares in a Merkle-tree, certifies the root, and sends with each share a proof of membership, i.e., a Merkle tree path to the root. When a validator receives a share, it should verify the Merkle tree proof against the certified root before acknowledging the share. Disperse completes when there are N-F acknowledgements, guaranteeing that untampered shares are held by F+1 honest validators.

During Retrieve(tx-key), F+1 validators reveal individual shares, attaching the Merkle tree path to prove shares have not been tampered with. Note that F+1 shares can be validated by checking only one signature on the root. Validators use SS-combine() to try to reconstruct tx-key.

Then they post-verify that every subset of F+1 (untampered) shares sent to validators would have the same outcome. To do this, a validator doesn’t need to wait for missing shares nor try combinations of F+1 shares. Moreover, it doesn’t need to communicate with others. A validator simply generates missing shares and re-encodes the Merkle tree. Then, it compares the re-generated Merkle tree with the root certified by the sender. If the comparison fails, the dealer was faulty and the validator rejects tx. Binding holds because the post-verification outcome – succeed or fail – becomes fixed upon Disperse completion. Each validator arrives at the same outcome no matter which subset of F+1 (untampered) shares are input, thus ensuring Binding.

A variant of this scheme is to have the user commit to – and disperse – a simple vector of hashes of shares instead of a Merkle tree. Dispersing a hash vector (in full) incurs a higher communication complexity than dispersing a Merkle root (e.g., quadratic using [hbACSS, NDSS 2022]) as well as higher computational cost, but brings the overall Retrieve complexity down (to quadratic).

Properties:

No trusted setup is required.
Roughly 50μs and O(N²) overall communication for Disperse (O(N²) with a hash vector commitment). A user needs to send shares privately to individual validators accompanied by a Merkle proof.
Roughly 50μs and O(N² * log(N)) overall communication for Retrieve (O(N²) with a hash vector commitment), including post-verification, in a 6-out-of-16 scheme.

Approach 4: Hybrid

Even after Disperse has completed, both VSS and AVID-M may need to interact with a specific set of F+1 honest validators during Retrieve. This implies that the latency of Retrieve is impacted by this specific set of F+1 “shareholders” and not the speed of the fastest F+1 honest validators. Employing threshold cryptography removes this dependency but incurs a costly computation.

A Hybrid approach combines the benefits of threshold cryptography with AVID-M. In Hybrid, Retrieve works with (fast) secret-sharing during steady-state, and falls back to threshold cryptography, avoiding waiting for specific F+1 validators, during a period of network instability.

Disperse(tx-key) is implemented in two parts. First, a user applies AVID-M to send parties individual shares and proofs. Second, as a fallback, it sends validators E(tx-key). Once tx is committed to the total ordering, Retrieve(tx-key) has a fast track and a slow track. In the fast track, every validator that holds an AVID-M for tx-key reveals it. A validator that doesn’t hold an AVID-M share for tx-key reveals a threshold key decryption share. In the slow track, validators may give up on waiting for AVID-M shares and reveal threshold key decryption shares, even if they already revealed AVID-M shares.

Post-verification after Retrieve (either the fast or slow paths) checks both the AVID-M post-verification and that E(tx-key) is consistent with the AVID-M dispersal. More specifically, a validator simply re-encrypts tx-key and re-encodes the AVID-M Merkle tree after reconstruction. It compares both with the sender’s. If the comparison fails, the dealer was faulty and the validator rejects tx. Once again, the post-verification outcome – succeed or fail – becomes fixed upon Disperse completion. Each validator arrives at the same outcome no matter which scheme and which subset of F+1 (untampered) shares are input, thus ensuring Binding.

Properties:

Requires trusted setup or a (computationally costly) distributed setup of threshold encryption.
Roughly 360μs and O(N² * log(N)) (O(N²) with a hash vector commitment) overall communication for Disperse in a 6-out-of-16 scheme. A user needs to send AVID-M shares privately to each validator. A user piggybacks E(tx-key) on the broadcast of tx with no extra messages.
Roughly 50μs and O(N² * log(N)) (O(N²) with a hash vector commitment) overall communication for a fast Retrieve in a 6-out-of-16 scheme, 3500μs for a slow Retrieve. Post-verification takes about 400μs in both.
Retrieve is optimistically fast and additionally, may progress at the speed of the fastest F+1 honest validators.

Fino: Blind Order-Fairness on a DAG

In DAG-based consensus protocols (the subject of a previous post), validators broadcast blocks of yet-unconfirmed transaction digests via a reliable and causally ordered transport. The advent of the DAG approach is that every consensus message has direct utility towards forming a total ordering of committed transactions.

A DAG transport exposes two APIs, broadcast() and deliver(). When a validator delivers a broadcast message into its local DAG, it has the following guarantees:

Reliability: there are copies of the message that eventually, all honest validators can download it
Non-equivocation: messages by each validator are numbered. If an honest validator delivers some message as the k’th from a particular sender, then the message is authenticated by its sender and other honest validators deliver the same message as the sender k’th message.
Causal ordering: the message carries explicit references to messages which the sender has previously delivered (including its own). Predecessors are delivered locally before the message is delivered.

Note that the DAGs at different validators may be slightly different at any moment in time. This is inevitable in a distributed system due to message scheduling. However, a DAG-based consensus protocol allows each validator to interpret its local DAG, reaching an autonomous conclusion that forms total ordering.

Reliability, Non-equivocation, and Causal Ordering greatly simplifies Blind Order-Fairness implementation:

When tx is broadcast, the DAG transport collects acknowledgment from N-F validators that they received shares of tx-key. This guarantees that if tx is a candidate for commit ordering, it has already completed the Disperse phase.
Share Retrieve starts automatically and autonomously when a validator observes that tx becomes committed in its local DAG.
Broadcasting shares into the DAG allows everyone to observe tx being opened, even if they did not actively participate in Retrieve. Furthermore, it allows stalling consensus progress until all pending committed transactions have F+1 shares revealed.

Overview of Fino

Fino incorporates Blind Order-Fairness protection into a BFT protocol for the partial synchrony model, riding on a DAG transport.

To build Blind Order-Fairness on a DAG, we wanted a simple baseline DAG-BFT algorithmic foundation. Fino has minimalist and purist approach emphasizing the following key tenets:

Zero DAG delay – Fino never requires the DAG to wait for input that depends on consensus steps/timers, and avoid any sort of rigid constraints on DAG structure (e.g. layering).
Simple – Fino is quite possibly the simplest way to embed BFT consensus in a DAG.
Partial synchrony – The solution guarantees that when the network is stable, only two broadcast latencies are required to reach a consensus decision. An ordering decision commits in a batch all the transactions that have accumulated in the DAG.

It should be noted that our Disperse/Retrieve framework can possibly be built on other DAG-BFT systems.

Views. The protocol operates in a view-by-view manner. Each view is numbered, as in view(r), and has a designated leader known to everyone.

View change. A validator enters view(r+1) when two conditions are met, viewA and viewB:

viewA is satisfied when the local DAG of a validator contains F+1 valid votes on proposal(r) or 2F+1 valid complaint(r) on view(r).
viewB is satisfied when every committed transaction tx in the local DAG has completed Disperse(tx-key). Note that viewB prevents progress without opening committed transactions.

Proposing. Validators periodically pack encrypted transactions into a batch and use the DAG transport to broadcast them. When a leader enters a new view(r), its broadcast is interpreted as proposal(r). Implicitly, proposal(r) suggests to commit to the transaction total-ordering all the messages in the causal history of the proposal. A leader’s proposal(r) is valid if it is justified in entering view(r).

Voting. When a validator sees a valid leader proposal, it broadcasts vote(r). A validator’s vote(r) is valid if it follows a valid proposal(r).

Committing. Whenever a leader’s proposal(r) has F+1 valid votes in the local DAG, the proposal and its causal history become committed. A validator processes a committed proposal(r) as follows:

Ordering Commits. Let r’ be the highest view r’ < r for which proposal(r’) is in the causal history of proposal(r). Recursively, proposal(r’) is ordered. The remaining causal predecessors of proposal(r) which have not yet been ordered are appended to the committed sequence (within this batch, ordering can be done using any deterministic rule to linearize the partial ordering into a total ordering.)

Share revealing. For each newly committed transaction tx, the Retrieve(tx-key) procedure is started. Shares are piggybacked on DAG broadcasts that causally follow the decision. A successful Retrieve reconstructs tx-key and uses it to decrypt tx; Retrieve might fail if the sender of tx misbehaved, in which case tx is rejected.

Complaining. If a validator gives up waiting for a commit to happen in view(r), it broadcasts complaint(r). Note, a vote(r) by a validator that causally follows a complaint(r) by the validator, if exists, is not interpreted as a valid vote.

A Note on Happy-path Latency. During periods of stability, there are no complaints about honest leaders by any honest validator. If tx is proposed by an honest leader in view(r), it will receive F+1 votes and become committed within one network latency. Within one more network latency, honest validators will post a message containing a share for tx. Everyone will be able to apply Retrieve(tx-key) and either open tx or reject it. In summary, in a happy path, blindly committing and opening tx happens three network latencies after it is submitted.

Example scenarios. Figure 1 illustrates a couple of Fino scenarios. In the first view (view(r)), proposal(r) becomes committed. The commit sets an ordering for every transaction tx in the causal past of proposal(r), and enables their Retrieve.

A slightly more complex scenario occurs in view(r+1). The view expires because parties do not observe a leader’s proposal becoming committed and they broadcast complaints. Entering view(r+2) is enabled by 2F+1 complaints about view(r+1). When proposal(r+2) itself becomes committed, it indirectly commits proposal(r+1) as well. Thereafter, Retrieve is started for every pending committed transaction, including those in proposal(r+1) and proposal(r+2).

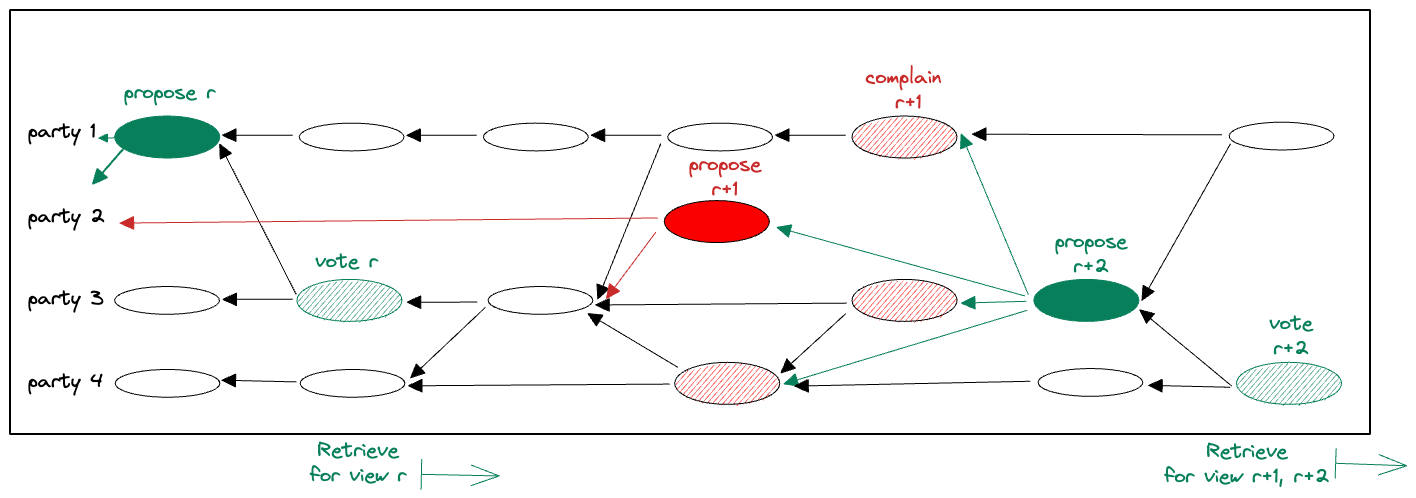
Illustrating a few Fino scenarios — Figure 1: A commit of proposal(r) is followed by Retrieve. A commit of proposal(r+2) causes an indirect commit of proposal(r+1), followed by Retrieve of both.

Acknowledgments

Special thanks to Nibesh Shrestha for coming up with the idea of using hash-vector commitment in the AVID-M setting and exploring methods for implementing it.

Many thanks to Soumya Basu, Christian Cachin, Ari Juels, Mahimna Kelkar, Oded Naor, and Nibesh Shrestha for comments that helped improve this post.

The post MEV Resistance on a DAG appeared first on Chainlink Blog.

3y ago•

bullish:

1

bearish:

0

Share

Chainlink

Constellation

Manage all your crypto, NFT and DeFi from one place

Securely connect the portfolio you’re using to start.

Related News

Crypto2...

•

Crypto2Community

Best Cryptocurrencies to Invest in Today, December 29 – ETH, BCH, LINK

bullish:

0

bearish:

0

CoinCu...

•

CoinCu

Whales Accumulate LINK with Multi-Million Withdrawals from Binance

bullish:

1

bearish:

0

Captain...

•

CaptainAltcoin

Chainlink (LINK) Price Shows a Quiet Bullish Setup After Months of Decline

bullish:

0

bearish:

0

Blockch...

•

BlockchainReporter

LINK Whale Pulls Over $8.5M From Binance in Two Days, Bringing Fresh Market Attention

bullish:

0

bearish:

0